以前、混合事例紹介にて混合性は粒径差だけではなく流動性の影響も受けることを検証しました。（→[混合事例紹介]_混合性と粒径差の関係）

流動性を指標として用いるにあたって、わかりやすい数値で表す必要があります。

しかし何μmというように簡単に数字で表現できる粒径とは異なり、「流れやすさ」を数値で表す方法は一般的ではありません。

そこで今回は流動性を数値で表す方法についてご紹介します。

 

Carrの流動性指数

Carrの流動性指数とはR.L.Carr氏が提唱した概念で、粉体を扱う業界内では良く知られており、専用の評価装置も市販されています。

Carrの流動性指数では粉体の流動性を「安息角」「圧縮度」「スパチュラ角」「凝集度(または均一度)」の4項目で評価し、数値化します。

各項目が0～25pt.で、合計100pt.の指数となり、数値が高いほど流動性が高いことを表します。

以下で各項目について説明します。

 

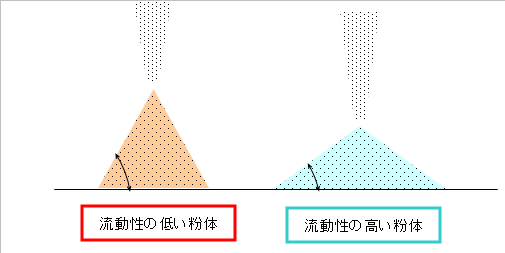
安息角（図-1）

自然に堆積した粉体が形成する山の斜面と水平面がなす角度のことで、粒子間の摩擦や粒子間の運動の抵抗を表す指数です。

流動性が高いほど山が崩れやすくなるので、安息角は小さくなります。

 

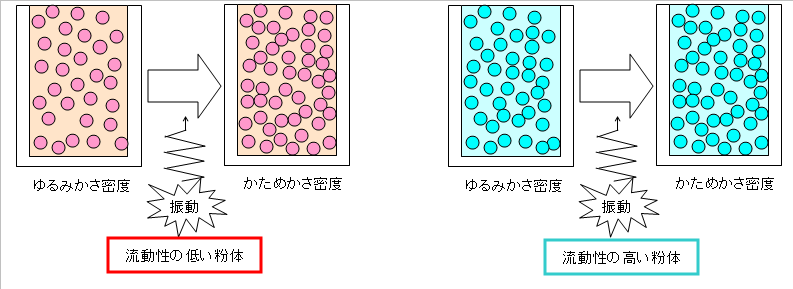
圧縮度（図-2）

容器に緩く充填した「ゆるみかさ密度 ρ_A」と容器に振動等を与えながら充填した「かためかさ密度 ρ_B」から次式を用いて算出します。

$$圧縮度=\frac{{ρ_B-ρ_A}\times{100}}{ρ_A}$$
流動性が高いほど充填性が高く、ゆるみかさ密度とかためかさ密度の差が小さくなるので、（つまり振動等を加えなくても、よく充填されるので）圧縮度は小さくなります。

 

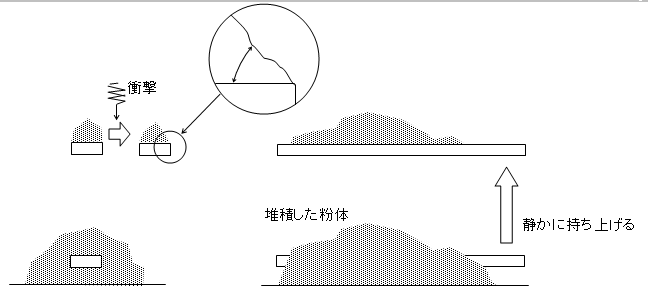
スパチュラ角（図-3）

堆積した粉体に平板を水平に埋め込み、垂直方向へ静かに持ち上げた際に形成される山と平板のなす角度です。

持ち上げた後に一定の衝撃を与えて、若干山が崩れた状態で角度を測定します。

安息角と同じく、流動性が高いほどスパチュラ角は小さくなります。

 

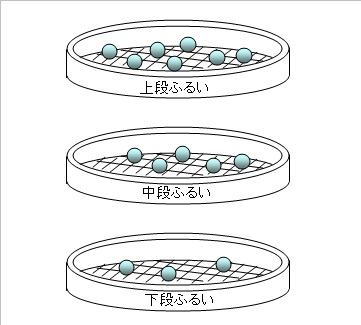
凝集度（均一度）（図-4）

３種類の目開きのふるいを目開きの小さい順に下から重ね、試料を最上段に乗せて振動を与えた時、

各ふるいに残った試料の量を基に算出します。

$$凝集度=\frac{{w_1+\frac{3}{5}w_2+\frac{1}{5}w_3}\times{100}}{w}$$

\(w\)：試料総量、\(w_1\)：上段に残った試料、\(w_2\)：中段に残った試料、\(w_3\)：下段に残った試料

流動性が高いほど、上の段のふるいに試料が残りにくいので凝集度は小さくなります。

そのためあまり流動性が高い粉体を使用すると、ほとんどの粉が下まで落ちてしまい、正しく測定することが難しくなります。その場合は均一度を評価します。

均一度は、粒度分布測定から得られた累積分布曲線寄り60%径 X₆₀及び10%径 X₁₀を求め、下式を用いて算出します。
$$均一度=\frac{X_{60}}{X_{10}}$$

 

以上の試験から得られた数値を表-1に示す換算表に当てはめて流動性指数を算出します。

 

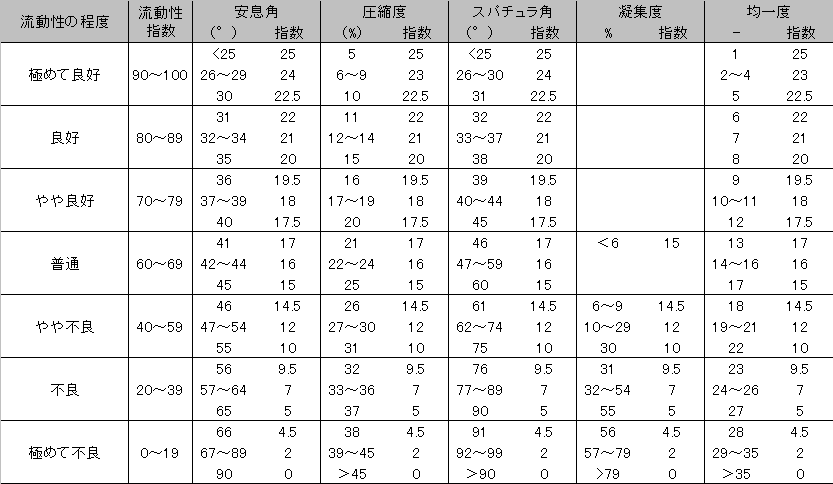
尚、弊社では市販の評価装置ではなく、簡易な器具を使用して流動性の評価を行っておりますので社内で評価した粉体間での再現性は取れておりますが、市販の機器を使用した場合の指数とは必ずしも一致しません。